Дробная часть вещественного числа (функция FractionalPart)
Упражнение 3.4.
Пусть:
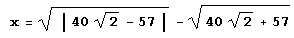
С колько у этого числа нулей следует сразу после десятичной точки?
Решение.
Вот самое простое решение. Сначала вводим определение числа.
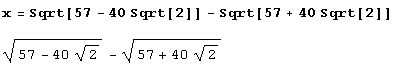
Теперь нужно вычислить число с такой точностью, чтобы найти хотя бы один ненулевой знак после запятой. Итак, попробуем.
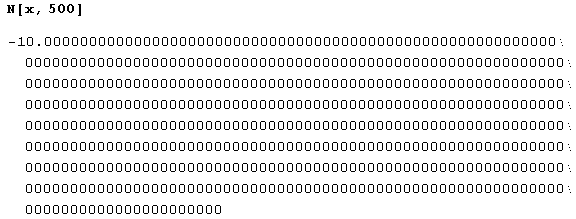
Да это ж предыдущий случай! Мы уже знаем, как с этим справиться.
Видите ли… Как бы вам это популярнее объяснить, пока продолжаются вычисления… Отличие от предыдущего случая состоит в том, что в предыдущем случае мы убедились, что 1 действительно является целой частью исследуемого числа. В данном же случае мы лишь предполагаем, что число -10 является целой частью числа х. Но -10 может ведь оказаться и отрицательным, а тогда логарифм окажется комплексным. Это, впрочем, совсем не страшно, мы лишь должны будем вычислить логарифм х+11. Вот и всего-то… Да, но что-то наши вычисления слишком затянулись… Понимаете, тут я должен сделать еще одно разъяснение. Видите ли, чтобы вычислить логарифм, нужно проделать некоторые вычисления, и в нашем случае с довольно высокой точностью. И успех эти вычисления принесут лишь тогда, когда будет обнаружено, что аргумент логарифма (число х+10) отличен от нуля… А в данном случае для этого недостаточно даже вычисления более чем двух с половиной миллионов знаков. Видите ли, бывает же, что дроби сокращаются, а радикалы взаимно уничтожаются. Вот в данном случае как раз х+10 = 0, потому что х= -10. Данное число целое! Давайте попробуем убедиться в этом.
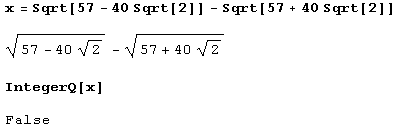
Возможно, вы подумали, что автор хотел обвести вас вокруг пальца! Число все-таки оказалось нецелым! Просто система Mathematica не смогла вычислить достаточное количество знаков, и автор решил упростить себе задачу. Увы, если вы согласились с тем, что число нецелое, совершили довольно распространенную ошибку. Не потому, что оно целое, а потому, что так проверять нельзя. Предикат IntegerQ[x] может принимать значение False даже для целого аргумента. Он проверяет не само число, а его внутреннее представление. Этот предикат принимает значение True только в том случае, если внутреннее представление числа имеет заголовок Integer. Вот как лучше проверять.
Как видите, все ответы тавтологичны. И в данном случае вопрос так и не прояснился… Да, система Mathematica не всегда может то, с чем справляется даже школьник:
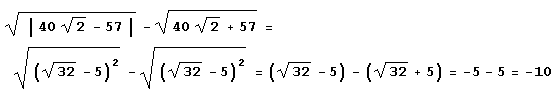
Теперь уж действительно ясно, что число целое. Конечно, придумать таких примеров можно великое множество. И проблема здесь не в коварстве авторов задачников, а в том, что не существует алгоритма (в классическом смысле), который для любого вещественного числа мог бы решить вопрос о том, равно оно нулю или нет. Существует специально разработанный математиками конструктивный анализ, в котором числовой континуум состоит не из обычных вещественных чисел, а из конструктивных. Для конструктивного вещественного числа всегда разрешим вопрос о том, равно ли оно нулю. Конструктивный континуум – та основа, на которой строятся другие объекты конструктивного анализа, например функции. Однако в конструктивном анализе изучаются не любые функции (отображения конструктивного континуума в себя), а только конструктивные. Несмотря на некоторое сходство, свойства конструктивных объектов отличаются подчас радикально.