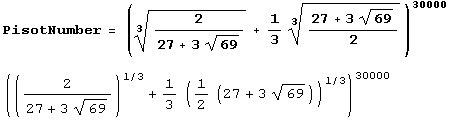Дробная часть вещественного числа (функция FractionalPart)
Да, а как же все-таки решить задачу? Ну, в данном случае это совсем несложно.

Почему же все-таки я подчеркиваю, что решить задачу несложно именно в данном случае? Вспомните пример с е '"". Там проблема была в том, что вычисленные десятичные приближения заканчивались девятками. А если бы и в этом примере цифры в конце оказались девятками, мы бы не смогли решить, верные ли они. (Именно для того, чтобы избежать округления и убедиться, что последняя цифра не девятка, мы и распечатываем k+1 цифру – k требуемых по условию задачи и одну запасную. Если бы запасная цифра оказалась девяткой, пришлось бы выводить еще несколько запасных цифр, пока не обнаружили бы отличную от 9.) Конечно, мы могли бы увеличить разрядность, но что если бы мы повстречали участок, сплошь состоящий из нескольких миллионов девяток? Может быть, это верные цифры, а может быть, нам просто не хватило точности, и в каком-то миллионе затерялась та единичка в переносе, добавление которой превращает все эти миллионы девяток в миллионы нулей? Вот оно коварство бесконечных десятичных дробей!
Из этого можно извлечь несколько уроков. Во-первых, выполняя действия над вещественными числами, нужно тщательно следить за точностью. Во-вторых, для применения таких функций, как FractionalPart, иногда необходима существенно более высокая разрядность, чем та, которая обеспечивается системой автоматически. В-третьих, иногда перестановка функций позволяет упростить программу. И, наконец, в-четвертых, вещественные числа иногда способны преподносить сюрпризы вроде девяток в конце вычисленных значений или необъятного количества ведущих нулей в начале дробной части. Тогда даже на простые вопросы вроде целое ли это число или конечная ли эта десятичная дробь ответить бывает чрезвычайно трудно. Ведь чем точнее удается приблизить бесконечную дробь рациональными числами, тем больше шансов на то, что она представляет собой число трансцендентное…
Упражнение 3.2 (число Пизо).
Вычислите 5555 десятичных цифр числа Пизо.
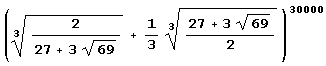
Сколько у этого числа нулей следует сразу после десятичной точки? Решение. Вот самое простое решение. Сначала вводим определение числа.