Числа Фибоначчи и цепные дроби
Давайте разложим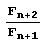 
(здесь Ft – /-е число Фибоначчи) в цепную дробь.
Как видите, количество звеньев разложения дроби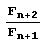 
равно n, причем последнее звено равно 2, а все предшествующие ему (если они есть) – 1. Этим свойством обладают только дроби 
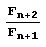никакая другая дробь такого разложения не имеет.
Вообще, выражения, содержащие числа Фибоначчи, доставляют подчас примеры чисел, разложения которых в цепные дроби обладают весьма интересными свойствами.
Пример 3.2.
Давайте определим следующую функцию.
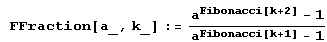
А теперь давайте попытаемся представить несколько ее значений в виде цепных дробей. Положим, например, а = 2, k = 15. Вот результаты.
