Числа Фибоначчи и цепные дроби
А теперь давайте возьмем логарифмы по основанию 2.
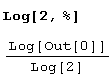
Если и это вам ничего не напоминает, взгляните вот на это.
Table[Fibonacci [n],{n,15.2,-1}] {610.377.233.144.89.55.34.21.13.8.5.3.2.1}Так что все звенья цепной дроби (кроме последнего), в которую разлагается число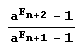 
представляют собой степени числа а, показателями которых служат числа Фибоначчи Fn, Fn-1, Fn-2,,…, F2, записанные в обратном порядке! То же самое имеем и для а = 3, k = 25.
Последний элемент цепной дроби, как видим, равен n+1. Конечно, фокус основан на тождестве:
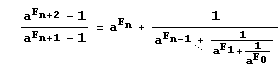
Хотя тождество справедливо для всех я, таких, что aFk =1 (k = 0, 1,…, n+1), именно для целых а правая часть будет "настоящей" цепной дробью.
Здесь целая часть выделена полужирным, а остальные элементы курсивом через один, чтобы их было легче отличить. Видно, как быстро убывают элементы дроби. Но вот если основание а не является целым числом, картина может измениться кардинально.