Иллюстрированный самоучитель по Mathematica 5

Целая часть вещественного числа (функции Floor и IntegerPart)

Всякое вещественное число представляет собой сумму его целой и дробной частей:

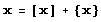
Есть множество способов преобразования вещественных чисел в целые. Но важнейшими из них являются округление к целому числу и отбрасывание дробной части.

Округление к ближайшему целому, не превосходящему х: функция Floor[x]

Функция Floor [х] представляет собой наибольшее целое, не превосходящее х.

Именно функция Floor в математике и называется целой частью числа и обычно обозначается через [х]. Заметьте, что эта функция отсекает дробную часть только неотрицательных чисел. Для отрицательных нецелых чисел ее работа иллюстрируется следующим примером.

Поэтому если необходимо просто отбросить дробную часть, лучше воспользоваться функцией IntegerPart.

Отбрасывание дробной части: функция IntegerPart

Функция IntegerPart просто отбрасывает дробную часть.

"Потолок" вещественного числа – округление к наименьшему целому, не превосходящему х: функция Ceiling

Выражение Ceiling [х] представляет собой наименьшее целое, которое не меньше х.

Округление вещественного Числа: функция Round

Функции Floor и Ceiling позволяют округлить вещественное число к меньшему или большему целому. Иногда же нужно выполнить округление к ближайшему целому. Именно для этого и предназначена функция Round.

Однако числа, дробная часть которых равна.5, имеют два ближайших целых. Такие числа функция Round округляет к ближайшему четному целому.