Иллюстрированный самоучитель по Mathematica 5

Комплексные числа

Мнимая единица

На специальной панели символов системы Mathematica имеется мнимая единица, но иногда ее удобно ввести просто как букву I или даже как \[Imaginaryi] или \[ImaginaryJ]. Вот примеры.

Вещественная часть комплексного числа: функция Re

Это совсем незамысловатая функция, возвращающая вещественную часть комплексного числа.

Заметьте, что в последнем примере вещественность а и b не предполагается.

Мнимая часть комплексного числа: функция Im

Тоже совсем незамысловатая функция, возвращающая мнимую часть комплексного числа.

Заметьте, что в случае Im[a+b I] вещественность а и b не предполагается – в отличие от случая, когда используется функция ComplexExpand.

Аргумент комплексного числа: функция Arg

Функция Arg[z] возвращает аргумент комплексного числа z.

Вот как, например, можно получить аргументы корней четвертой степени из 1.

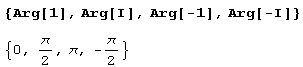
Возвращаемый угол всегда по абсолютной величине не превосходит n.

Сопряженное комплексное число: функция Conjugate

Выражение Conjugate [z] представляет собой сопряженное комплексное число z. Вот как, например, можно получить число, сопряженное к х+I у.

Заметьте, что х и у предполагаются комплексными.

Резюме

Мы рассмотрели основные числовые системы, предусмотренные в системе Mathematica. Они полностью охватывают классическую математику. Благодаря такому богатству система Mathematica может помочь в решении практически любых математических задач. Но благодаря этому же богатству при решении задач можно столкнуться с теми же проблемами, что и в математике. И потому решение исследовательских задач с помощью системы Mathematica может потребовать основательного знакомства с методологией применения данной системы в конкретной области науки и техники. Конечно, по высказыванию Гаусса, математика – царица всех наук. И потому в первую очередь следует освоить именно методологию применения системы Mathematica к решению математических задач. И начнем мы с царицы математики (по выражению того же Гаусса) – с арифметики.