Число как последовательность (список) цифр
Представление целого числа в виде списка цифр в нега-двоичной системе счисления
Если снование системы счисления b является отрицательным целым числом, меньшим -1, то такую систему называют нега-позиционной. Например, если b = -2, то такая система называется нега-двоичной, а если b = -4 – нега-четверичной, если b = -10 – нега-десятичной. Основным преимуществом этих систем является отсутствие знака перед отрицательными числами и, следовательно, отсутствие правил знаков. Дело в том, что всякое число любой из нега-позиционных систем с четным числом цифр отрицательно, а число, отличное от 0, с нечетным числом цифр – положительно. Особый интерес для конструкторов вычислительных машин представляет, конечно, нега-двоичная система. Однако если задать отрицательное основание (-2) в качестве второго параметра, функция IntegerDiglts "заругается".

Однако функция IntegerDigits позволяет определить функцию, которая сможет представить число в нега-двоичной системе.

И уж совсем просто определить функцию, которая по представлению числа в нега-двоичной системе находит его представление в десятичной системе:
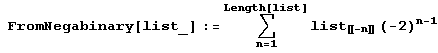
Вот пример (фактически мини-тест) применения обеих функций.

