Иллюстрированный самоучитель по Mathematica 5

Число как последовательность (список) цифр

Здесь уж точно можно определить, что нужны только две цифры! Правда, для этого нужно вникнуть в смысл выполняемой операции. Правда, функцию можно обмануть, но лишь с определенной точностью.

Второй способ обмана лучше.

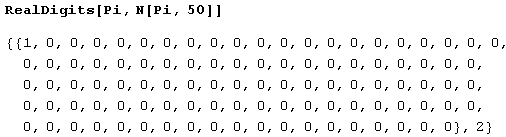
При первом же способе получим следующее.

Здесь Indeterminate – это цифра, в которой функция не уверена.

Представление рациональных чисел в виде списка цифр в системе счисления с произвольным основанием: функция RealDigits

Рациональные числа представляют собой конечные или периодические систематические дроби. Поэтому их представление в виде списка цифр в системе счисления с произвольным основанием имеет некоторые особенности. Проиллюстрируем их на примерах. Пусть имеем рациональное число 99/61. Оно представляется в виде периодической десятичной дроби. Вот как можно вычислить ее начало.

Теперь получим список цифр.

Пока ничего удивительного. Но ведь список цифр можно получить и проще.

Оказывается, в этом случае функция RealDigits соображает, что дробь получается периодическая, и находит ее период!