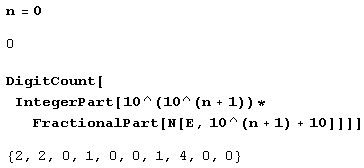Число как последовательность (список) цифр
"Цифромания" – как посчитать девятки в десятичном представлении е: функция DigitCount
Система Mathematica позволяет вычислить столько констант! С точки зрения "цифроманов" было просто преступно не воспользоваться этим и не узнать, например, как распределены единицы и нули в числах От 1 до 256, записанных в двоичной системе, или же не посчитать количество девяток в десятичном представлении основания натуральных логарифмов. Именно для этого (и многих других полезных вещей) как раз и предназначена функция DigitCount. Вызов DigitCount [n, b, d] возвращает количество цифр d (предполагается, что это цифра системы счисления с основанием b) в числе n, записанном в системе счисления с основанием b. Рассмотрим сначала простой пример. Вот как найти"представление числа 175! в системе счисления с основанием 25.

А вот как можно узнать, сколько раз в этом списке встречается цифра 14:

Но это еще что! Можно ведь даже построить график зависимости количества единиц в двоичном представлении n от и.
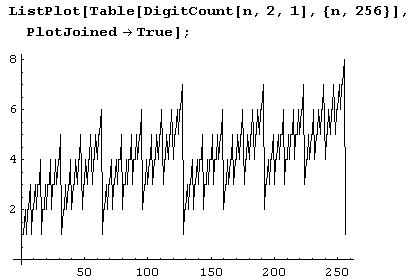
О, это настоящая музыка цифр! Но это еще не все: если третий параметр опущен, функция DigitCount посчитает количество вхождений каждой цифры в представлении числа π в системе счисления с основанием b. (Таким образом, получится список из b чисел.) При этом количество вхождений единицы стоит на 1-м месте в списке, двойки – на 2-м, цифры k (k > 0) – на k-м, а количество вхождений нуля – на последнем, 6-м. Если же опустить и второй параметр – основание системы счисления, то система счисления предполагается десятичной.
Вот как, например, можно сосчитать, сколько раз различные десятичные цифры входят в первые (после запятой) 10 знаков десятичного представления основания натуральных логарифмов.