Мультиномиальная логистическая регрессия
Для возрастной группы свыше 45 лет расчеты будут выглядеть следующим образом:
g1 = -0.333 + 0 = -0.333
g2 = 0.376 + 0 = 0.376
gз=0
ехр (g1) – ехр (-0.333) = 0.717
ехр (g2) * ехр (0.376) = 1.456
ехр (g3) = ехр (0) = 1
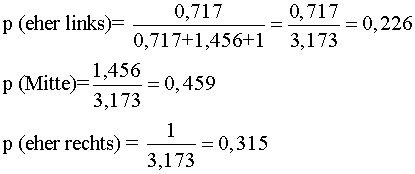
Если выразить полученные показатели в процентах, то и здесь так же наблюдается полное согласование с соответствующими процентными показателями таблицы сопряженности.
Следует отметить, что только в случае наличия лишь одной независимой переменной, как в приведенном примере, проведение расчета с применением столь громоздкого метода, как многозначная логистическая регрессия, является достаточно бессмысленным – все соотношения могут быть выяснены проще, при помощи таблиц сопряженности. Поэтому мы введем в рассмотрение еще одну дополнительную переменную – переменную schule (образование).
- В диалоговом окне Multinomial Logistic Regression (Мультиномиальная логистическая регрессия) поместите переменную schule вместе с переменной Alter в поле факторов.
- В диалоговом окне Multinomial Logistic Regression: Statistics (Мультиномиальная логистическая регрессия: Статистики) активируйте дополнительные опции Cell probabilities (Вероятность по ячейкам) и Likelihood ratio test (Тест отношения правдоподобия) и начните расчет вновь.
Таблица теста коэффициентов правдоподобия содержит изменения функции правдоподобия для случая, когда исключается соответствующий главный действующий фактор; эти изменения выражаются через соответствующие значения теста %2 (хи-квадрат). Выдаваемый уровень значимости р < 0.001 указывает на то, что оба фактора (возраст и школьное образование) оказывают очень значимое влияние на зависимую переменную (политическая самооценка).
Model Fitting Information (Информация о приближении, обеспечиваемой моделью)
| Model (Модель) | -2 Log likelihood (-2 логарифмическое правдоподобие) | Chi-square (Хи-квадрат) | df (степень свободы) | Sig. (Значимость) |
| Intercept Only (Только постоянное слагаемое) | 252.208 | |||
| Final (Окончательно) | 93.429 | 158.779 | 6 | 0.000 |
Likelihood Ratio Tests (Тест отношения правдоподобия)
| (Результат) | -2 Log Likelihood of Reduced Model (-2 логарифмическое правдоподобие для сокращенной модели) | Chi-square (Хи-квадрат) | df (Степень свободы) | Sig. (Значимость) |
| Intercept (Постоянное слагаемое) | 93.429 | 0.000 | 0 | 0 |
| ALTER (Возраст) | 171.496 | 78.067 | 2 | 0.000 |
| SCHULE (Образование) | 178.489 | 85.060 | 4 | 0.000 |
- The chi-square statistic is the difference in -2 tog-likelihoods between the final model:-~d a reduced model. The reduced model is formed by omitting an effect from the final model. The null hypothesis is that all parameters of that effect are 0 (Статистика хи-квадрат отображает различие -2 логарифмического правдоподобия между окончательной моделью и усеченной моделью. Суть расчета усеченной модели сводится к тому, что из окончательной модели исключается один фактор влияния. Нулевая гипотеза соответствует обнулению всех параметров параметрических оценок данного фактора влияния).
