Взвешенное оценивание (оценка с весами)
В данном примере мы имеем дело с группами случаев, разделенными по годам возраста, для которых независимая переменная имеет всегда одно и то же значение. Исходя из значений зависимой переменной сопоставленных каждому случаю, можно определить дисперсию; обратное значение этой дисперсии применяется обычно в качестве весового фактора для соответствующего случая.
Если подобной группировки данных нет, то пытаются выявить такую связь между дисперсией и переменной, чтобы степень дисперсии была пропорциональна значению данной переменной. При поиске так называемых весовых переменных речь идет о независимой переменной или, если их много, – об одной из независимых переменных. В приведенном примере такой переменной, очевидно, является независимая переменная Alter, по которой и можно проследить изменение дисперсии.
Целью анализа сначала является определение наилучшей возможной степени р. а затем подсчет веса для каждого случая, причем вес для значения переменной х определяется как:
1/хp
- Выберите в меню Analyze (Анализ) › Regression…(Регрессия) › Weight Estimation… (Взвешенное оценивание)
Откроется диалоговое окно Weight Estimation (Взвешенное оценивание).
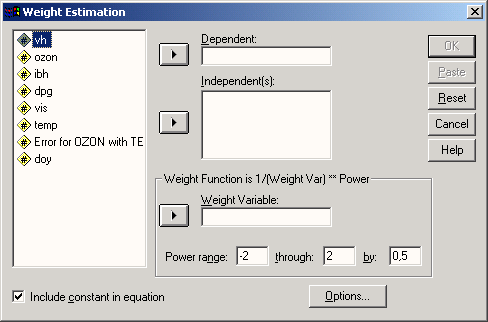
Рис. 16.27: Диалоговое окно Weight Estimation (Весовая цепка)
- Перенесите переменную staedte в поле зависимых переменных, а переменную Alter в поля для независимых и для весовых переменных. Согласно с установками по умолчанию оптимальная степень вычисляется в пределе от -2 до 2 с шагом 0.5; измените шаг на 0.2.
- Щелкните на кнопке опций и в появившемся диалоговом окне активируйте опцию Save best weight as new variable (Сохранить лучший вес, как новую переменную).
Результаты расчета, вывод которых производится в старой табличной форме, выглядят следующим образом:
| Source variable | .. ALTER | Dependent variable.. STAEDTE | |
| Log – likelihood | Function =-116.950816 | POWERvalue= -2.000 | |
| log – likelihood | Function =-115.170919 | POWERvalue= -1.800 | |
| Log – likelihood | Function =-113.434617 | POWERvalue= -1.600 | |
| Log – likelihood | Function =-111.746484 | POWERvalue= -1.400 | |
| Log – likelihood | Function =-110.111706 | POWERvalue= -1.200 | |
| Log – likelihood | Function =-108.536154 | POWERvalue= -1.000 | |
| Log – likelihood | Function =-107.026465 | POWERvalue= -0.800 | |
| Log – likelihood | Function =-105.590111 | POWERvalue= -0.600 | |
| Log – likelihood | Function =-104.235463 | POWERvalue= -0.400 | |
| Log – likelihood | Function =-102.971835 | POWERvalue= -0.200 | |
| Log – likelihood | Function =-101.809499 | POWERvalue= 0.000 | |
| Log – likelihood | Function =-100.759655 | POWERvalue= 0.200 | |
| Log – likelihood | Function =-99.834344 | POWERvalue= 0.400 | |
| Log – likelihood | Function =-99.046284 | POWERvalue= 0.600 | |
| Log – likelihood | Function =-98.408623 | POWERvalue= 0.800 | |
| Log – likelihood | Function =-97.934594 | POWERvalue= 1.000 | |
| Log – likelihood | Function =-97.637078 | POWERvalue= 1.200 | |
| Log – likelihood | Function =-97.528092 | POWERvalue= 1.400 | |
| Log – likelihood | Function =-97.618231 | POWERvalue= 1.600 | |
| Log – likelihood | Function =-97.916114 | POWERvalue= 1.800 | |
| Log – likelihood | Function =-98.427890 | POWERvalue= 2.000 | |
| The Value of POWER Maximizing Log-likelihood Function = 1.400 | |||
Оптимальная степень оценивается при помощи логарифма функции правдоподобия; в данном случае максимальное значение получается при значении степени равном 1.4. Это значение используется для определения веса для каждого случая. К примеру, для трехлетнего ребенка вес равен:
1/(31.4)=0.2148
Весовые показатели были добавлены в исходный файл под переменной с именем wgt_1. Затем повторно был выполнен расчет регрессии. Корреляционный коэффициент при этом возрос до 0.90081, а мера определенности до 0.81146. Хотя эти изменения, а также изменение рассчитанных коэффициентов регрессии и констант незначительны, зато стала намного меньше соответствующая им стандартная ошибка.
