Операторы и функции. Арифметические операторы.
Арифметические вычисления с повышенной точностью
Важное достоинство систем символьной математики – выполнение арифметических вычислений с произвольными разрядностью и точностью. Хотя на деле они ограничены объемом ОЗУ, но для современных компьютеров с объемом ОЗУ в единицы и десятки мегабайт вряд ли можно столкнуться со случаем, когда ограничения по разрядности и точности становятся существенными.
Следующие две функции, Rationalize [х] и Rationalize [x, dx], дают приближение для числа х в виде рациональных чисел. Вторая из этих функций задает приближение с заданной точностью dx.
Mathematica может работать с большими числами и выполнять определенные операции с очень высокой точностью. Примеры, приведенные на рис. 3.3, иллюстрируют эти возможности.
Как видно из примеров представления рациональных чисел, результат приближения зависит от заданной погрешности. Чем она меньше, тем большие значения целых чисел в числителе и знаменателе результата разыскивает система. Функция Rationalize открывает широкие возможности для разработки целочисленных алгоритмов вычислений, позволяя легко получать рациональные приближения для наиболее распространенных числовых констант – на рис. 3.3 примеры этого даны для числа 8.
Обратите внимание на последние два примера – вычисление факториала достаточно большого числа. Первый результат целочисленный: он занял целых три строки, но зато он точен. С помощью функции N [ехрг] результат всегда можно представить в виде большого вещественного числа – но приближенного. При этом может использоваться научная форма представления чисел – с мантиссой и порядком.
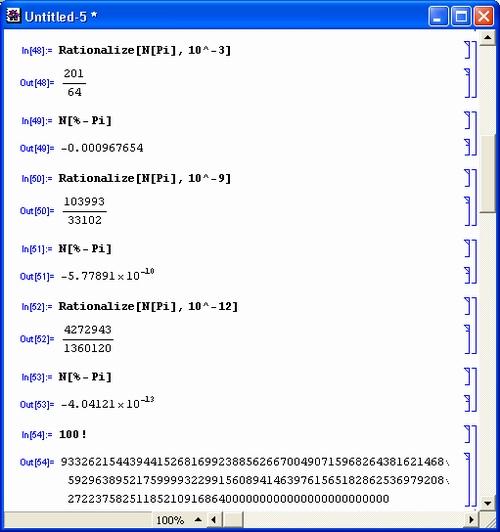
Рис. 3.3. Примеры представления чисел в разных формах
Укороченная форма записи арифметических операций
Спецификой систем Mathematica являются арифметические операторы с укороченной формой записи, объединяющие операцию присваивания с арифметической операцией. Эти довольно специфические операторы, хорошо известные пользователям языка С, представлены ниже вместе с соответствующими им функциями.
| Функция | Оператор | Назначение |
|---|---|---|
| Increment [i] | i++ | Увеличивает значение i на 1 после использования i в выражении |
| Decrement [i] | i – | Уменьшает значение i на 1 после использования i в выражении |
| Preincrement [i] | ++i | Увеличивает значение i на 1 до использования i в выражении |
| PreDecrement [i] | --i | Уменьшает значение i на 1 до использования i в выражении |
| AddTo[x,d] | x += dx | Прибавляет dx к х и возвращает новое значение х |
| SubtractFrom[x,dx] | x – = dx | Отнимает dx от х и возвращает новое значение х _ |
| TimesBy [х, с] | X **= 'С | Умножает х на с и возвращает новое значение х |
| DivideBy [х, с] | X /= С | Делит х на с и возвращает новое значение х |
Применение укороченных операторов делает запись математических выражений более короткой, хотя наглядность их при этом несколько снижается. Ниже представлены примеры выполнения укороченных арифметических операций.
| Ввод (In) | Вывод (Out) |
|---|---|
| i=0 | 0 |
| ++i; ++i; ++i | 3 |
| i=0; i++; i++; i++ | 2 |
| i=5 | 5 |
| – i | 4 |
| i=5 | 5 |
| i – | 5 |
| i – | 4 |
| x=5 | 5 |
| x+=0. 5 | 5.5 |
| x-=0. 5 | 5. |
| x*=2 | 10. |
| x/=5 | 2. |
