Дискретные функции единичного скачка и импульса (KroneckerDelta)
В подпакете KroneckerDelta системы Mathematica 3 заданы дискретные функции единичного скачка и единичного импульса:
- DiscreteStep [n] – возвращает единичный скачок при целом n=0;
- DiscreteStep [n1, n2,…] – функция многомерного единичного скачка;
- KroneckerDelta [n] – возвращает 1 при целом n=0 и 0 во всех других случаях;
- KroneckerDelta [n1, n2,…] – многомерная функция Кронекера.
Примеры использования этих функций в одномерном варианте представлены ниже:
<<DiscreteMath`KroneckerDelta` Table[DiscreteStep[n], {n, -3, 3}] {0, 0, 0, 1, 1, 1, 1} Table[DiscreteStep[n], {n, -3, 3, 1/2}] {0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 1} Table[KroneckerDelta[n], {n, -2, 2, 1/2}] {0, 0, 0, 0, 1, 0, 0, 0, 0} Sum[KroneckerDelta[n-a]f[n], {n, -Infinity, Infinity}] f[a] Sum[((KroneckerDelta[n] - KroneckerDelta[n-1]) -(KroneckerDelta[n-1] - KroneckerDelta[n-2])) f[n], {n, -Infinity, Infinity}] f[0]-2f[l] +f[2]Рисунок 11.17 иллюстрирует применение функции единичного скачка в двумерном случае.
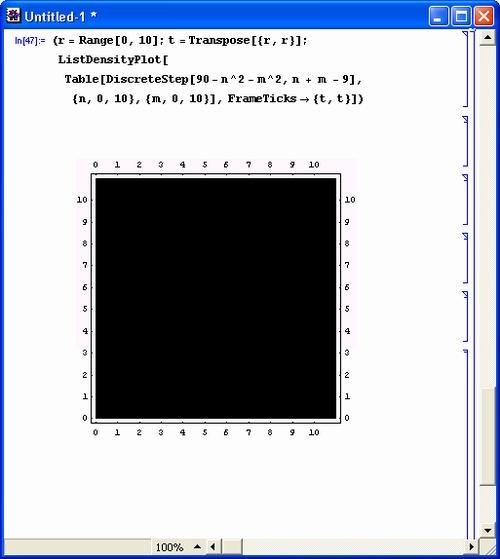
Рис. 11.17. Пример применения функции скачка в двумерном случае
В системе Mathematica 4 функция KroneckerDelta стала встроенной. В данный подпакет входят еще две функции:
- SimplifyDiscreteStep [ехрr] – упрощение выражения ехрг с функциями дискретного скачка;
- SimplifyKroneckerDelta [ехрг] – упрощение выражения ехрг с дельта-функцией Кронекера.
Действие этих функций демонстрируют следующие примеры:
DiscreteStep[n -1] (KroneckerDelta[n -2] + DiscreteStep[n, m] DiscreteStep[m -1]) // SimplifyDiscreteStep DiscreteStep[-1+m] DiscreteStep[-1+m] + KroneckerDelta[-2+n] (f[n] + KroneckerDelta[n]) DiscreteStep[n-l] // SimplifyKroneckerDelta DiscreteStep [ -1 + n] f [ n]