Численные расчеты (пакет NumericalMath). Аппроксимация аналитических функций (Approximations).
Пакет расширения NumericalMath содержит множество полезных функций для тех, кто имеет дело с численными расчетами. В их числе функции для выполнения высокоточных аппроксимаций рациональными функциями, численного интегрирования и дифференцирования, вычисления пределов функций, решения уравнений, разложения в ряд и т. д. Ниже описано подавляющее большинство функций этого расширения. Исключены лишь отдельные функции, представляющие ограниченный интерес и несложные для самостоятельного изучения (в подпакетах Butcher, Microscope и ComputerArithmetic).
Подпакет Approximations содержит ряд функций для улучшенной рациональной аппроксимации аналитических функций. Для рациональной интерполяции и аппроксимации функций по заданным значениям абсцисс служит следующая функция:
- Rationallnterpolation [f, {x,m, k}, {x 1 , x 2 ,…,.x m+k+1 } ] – возвращает аппроксимирующее функцию f выражение в виде отношения полиномов а степенью полинома числителя m и знаменателя k в абсциссах, заданных списком {x1, x 2 ,…, x m+jt+1 }.
Пример применения этой функции:
<<NumericalMath`Approximations` ril = Rationallnterpolation[Exp[x], {x, 2, 4}, {0, 1/3, 2/3, 1, 4/3, 5/3, 2}]Построим график погрешности аппроксимации, то есть график разности функции ril и Ехр [х] – он представлен на рис. 11.22.
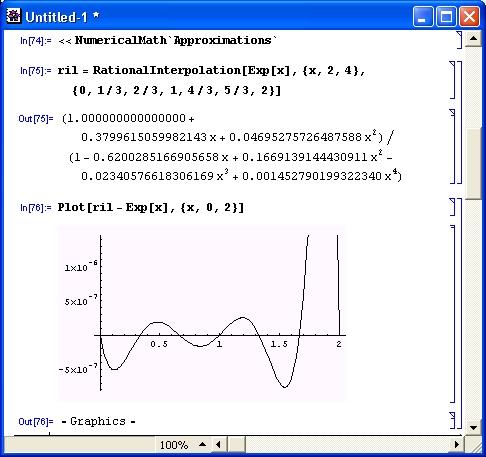
Рис. 11.22. График погрешности рациональной аппроксимации экспоненциальной функции
Нетрудно заметить, что если в центральной части области аппроксимации погрешность мала (менее 5-10-7), то у правого края она резко возрастает.
Представленная функция может использоваться и в иной форме:
Rationallnterpolation[f, {x, m, k},{x, xmin, xmax}]В данном случае выбор абсцисс осуществляется автоматически в интервале от xmin до mах. В отличие от первого случая, когда абсциссы могли быть расположены неравномерно, в данном случае расположение их будет равномерным. Приведем пример аппроксимации функции синуса в интервале от n до n:
ri2 = RationalInterpolation[Sin[x], {x, 3, 4}, {x, -Pi, Pi}]