Численные расчеты (пакет NumericalMath). Аппроксимация аналитических функций (Approximations).
Следует отметить, что малость абсолютной ошибки для ряда функций (например, тригонометрических) может приводить к большим относительным погрешностям в точках, где функции имеют нулевые значения. Это может привести к отказу от выполнения аппроксимации вследствие исчерпания числа итераций (опция Maxlterations по умолчанию имеет значение 20). Такой случай наблюдается, например, при исполнении следующей команды:
MiniMaxApproximation[Cos[x], {x, {1, 2}, 2, 4}]Делением функции на (x-Pi/2) можно исключить эту ситуацию:
MiniMaxApproximation[Cos[x]/(x-Pi/2),{*,{1!,2},2.4}] [[2.1]]График погрешности для этого примера представлен на рис. 11.26. Обратите внимание на то, что в этом примере погрешность аппроксимации не превышает (6…7) -10-10.
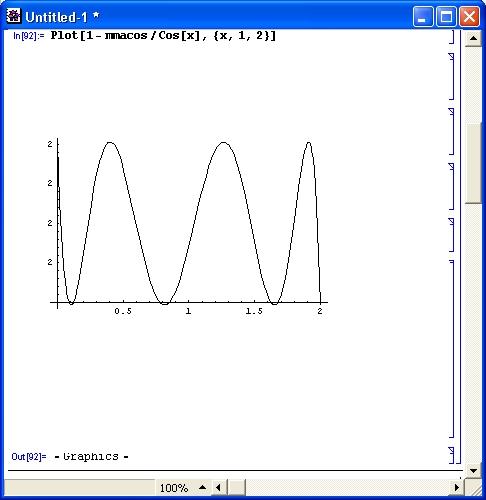
Рис. 11.26. График погрешности при минимаксной аппроксимации функции косинуса
В приложении дан список функций общей рациональной интерполяции (аппроксимации) для аналитических зависимостей, заданных параметрически. Примеры применения этого довольно редкого вида аппроксимации можно найти в справочной базе данных системы Mathematica. Там же можно найти дополнительные соображения по уменьшению погрешности аппроксимации.
