Иллюстрированный самоучитель по Mathematica 3/4

Численные расчеты (пакет NumericalMath). Аппроксимация аналитических функций (Approximations).

Из приведенных примеров ясно, что рациональная аппроксимация способна дать существенное уменьшение погрешности при некотором оптимальном расположении узлов аппроксимации и выравнивании погрешностей по абсолютной величине в точках минимумов и максимумов кривой погрешности. Это лежит в основе так называемой минимаксной аппроксимации. Она реализуется следующей функцией:

• MiniMaxApproximation[f,{x,{xmin,xmax},m,k}] – возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax:
• MiniMaxApproximation [f, approx, {x, {xmin, xmax},m, k} ] – возвращает рациональную функцию минимаксной аппроксимации f при степени полиномов числителя и знаменателя {m, k} ив интервале изменения х от xmin до xmax с возможностью выбора метода аппроксимации approx.

Эта аппроксимация использует итерационный алгоритм вычислений. Они начинаются с первого шага, на котором используется функция Rational Interpolation. Затем аппроксимация последовательно улучшается применением алгоритма Ремеза, лежащего в основе этого вида аппроксимации.

Функция MiniMaxApproximation возвращает два списка – первый с координатами абсцисс, при которых наблюдается максимальная погрешность, второй содержит рациональную функцию аппроксимации. Ниже представлен пример аппроксимации экспоненциальной функции:

Выделим формулу аппроксимации:

Теперь можно построить график погрешности аппроксимации (рис. 11.25).

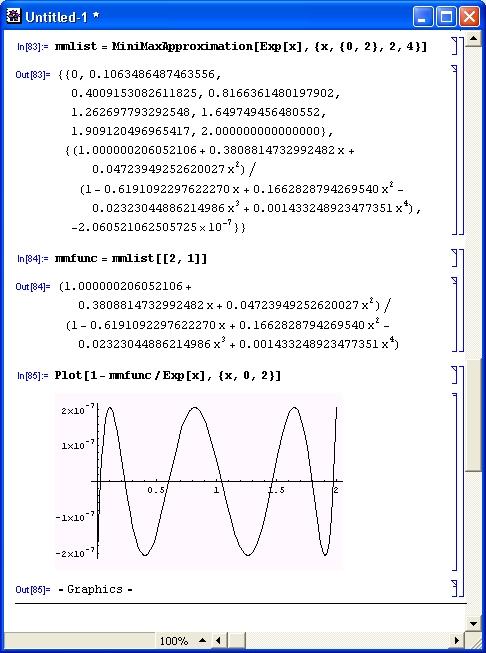
Рис. 11.25. График погрешности при минимаксной аппроксимации экспоненциальной функции