Вариационные методы (VariationalMethods)
Подпакет VariationaLMethods содержит функции для реализации вариационных методов. Напомним, что вариационные методы заменяют минимизацию функционала, заданного на некотором бесконечномерном линейном пространстве, задачами его минимизации на последовательности конечномерных подпространств. Функционал в системе Mathematica задается следующим образом:
F=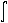 
f[u[x], u'(x),x]dx.
В данный подпакет включены следующие функции:
- VariationalD [f, u [х], х] – дает первую вариационную производную для функционала f одной переменной х;
- VariationalD [f, u [х, у,…], {х, у,…} ] – дает первую вариационную производную для функционала ряда переменных;
- VariationalD [f, {u [х, у,…], v [х, у],…}, {х, у,…} ] – дает список первых вариационных производных для функционала ряда переменных;
- EulerEquations [f, u [х], х] – дает равенство Эйлера при f с одной переменной;
- EulerEquations [f, u [х, у,…], {х, у,…} ] – дает равенство Эйлера при f с рядом переменных;
- EulerEquations [f, {u [х, у,…], v [х, у,…],…}, {х, у,…} ] – дает список с равенствами Эйлера при f с рядом переменных;
- Firstlntegral [ f, u [х], х] – дает первый интеграл с f, определенной для одной переменной х;
- Firstlntegral [f, {u [х, у,…],v [х, у,…],…}, {х, у,…} ] – дает первый интеграл при f с рядом переменных;
- Firstlntegral[u] – дает первый интеграл, ассоциированный с переменной и.
Применение данных функций поясняют следующие примеры:
<< Calculus`VariationalMethods` VariationalD[y[x] Sin[l+y`[x]], y[x], x] -Cost 1 +y[x]] y`[x] + Sin[l + y`[x]] d+y[x] y`[x]) EulerEquations[ m1^2 theta1[t]^2/2+m g 1 Cos[theta[t]], theta[t], t] -Im(gSin[theta[t]] + 1 theta''[ t]) == 0 Firstlntegrals[m(r`[t]^2+r[t]^2 phi`[t]^2)/ 2-U[r], r[t],phi[t], t] {Firstlntegral[phi] > -mr[ t]2 phi`[ t], Firstlntegral[t] > 1/2 (2U[r] + m (r[t]2phi`[t]2 + r^t]2)) }Помимо указанных функций подпакет содержит функцию VariationalBound для представления границ и значений функционала. Ввиду громоздкости записи параметров этой функции ограничимся примерами ее применения:
VariationalBound[(-u[r] D[r^2 u'[r],r]/r^2-2u[r]^2/r)r^2, u[r]^2 r^2,u[r], r,0,Infinity,(a-r)E^(-b r),a,b] {-0.25, (a > 2., b > 0.5}} VariationalBound[-u[x,y](D[u[x,y],x,2]+D[u[x,y],y,2]) -2u[x,y],u[x,y],x,-a,a,y,-a,a, (x^2-a^2)(y^2-a^2)(al+a2(x^2+y^2)),al,a2]С полными возможностями этой функции можно ознакомиться по справочной базе данных (раздел Add-ons).