Улучшенное вычисление пределов (Limit). Рациональная аппроксимация аналитических функций (Fade).
Пример осуществления экономичной рациональной аппроксимации показан на рис. 11.3. Здесь также дана визуализация аппроксимации в виде наложенных друг на друга графиков исходной и аппроксимирующей функций.
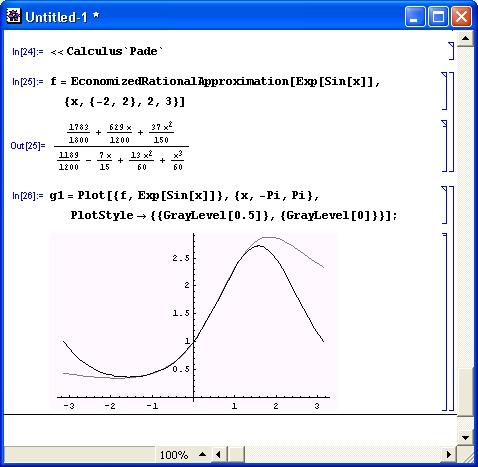
Рис. 11.3. Пример осуществления экономичной рациональной аппроксимации
Экономичная рациональная аппроксимация обычно позволяет получить приемлемую погрешность при меньшей степени полиномов числителя и знаменателя аппроксимирующей функции. В ограниченной области {xmin, xmax} эта аппроксимация нередко позволяет получить погрешность менее сотых долей процента (рис. 11.4). На этом рисунке показан график погрешности в виде разности между значениями аппроксимирующей и аппроксимируемой функций.
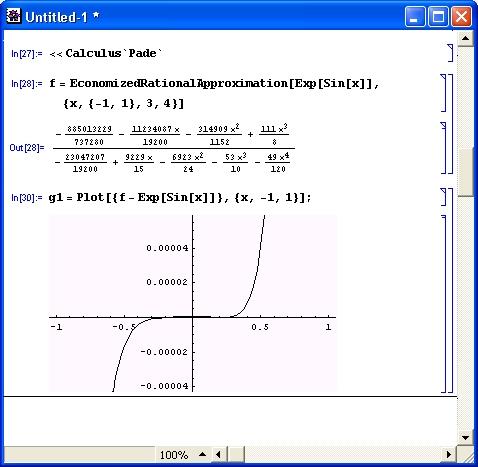
Рис. 11.4. Пример осуществления экономичной рациональной аппроксимации с построением графика погрешности
Несмотря на обширные возможности выбора средств аппроксимации, все же надо отметить, что они уступают таковым у конкурента системы Mathematica – Maple V R4/R5, где функций для осуществления аппроксимации больше.
