Улучшенное вычисление пределов (Limit). Рациональная аппроксимация аналитических функций (Fade).
Подпакет Limit не создает новых функций. Он просто переопределяет встроенную функцию Limit, так что ограничимся примерами его применения:
<< Calculus`Limit` Limit[E^x^x/ E^x^(2 x), x > Infinity] 0 Limit [E^x^x -E^x^ (2 x), x > Infinity] - бесконечность Limit[E:x ExpIntegralE[2, ArcTan[E^x] -Pi/2] -E^x -x, x > Infinity] 1 -EulerGamma -Iπ Limit[Zeta[l+x, v] -1/x, x > 0] -PolyGamma[0, v], Limit[x^0 PolyGamma[2,x], x > Infinity]. 0 Limit[x^2 PolyGamma[2,x], x > Infinity] -1 Limit[x^3 PolyGamma[2,x], x > Infinity] - бесконечностьРабота скорректированной функции наиболее эффективна при вычислении пределов от выражений, содержащих специальные математические функции, и пределов при х, стремящемся к бесконечности.
Рациональная аппроксимация аналитических функций (Fade)
Полиномиальная аппроксимация и обычное разложение функций в ряд Тейлора нередко дают слишком большую погрешность. Уменьшение ее возможно при представлении аппроксимирующей функции в виде отношения двух полиномов разной степени. В подпакете Fade определены две функции для рациональной аппроксимации Паде:
- Pade[f, {x,x0,m,k}] – возвращает выражение для аппроксимации Паде функции f(x) в окрестностях точки х0 в виде отношения двух полиномов степеней m и k;
- EconomizedRationalApproximation [f, {х, {xmin, xmax}, m, k} ] – возвращает выражение для осуществления экономичной рациональной аппроксимации функции f(x) в интервале {xmin, xmax} в виде отношения двух полиномов степеней m и k.
Аппроксимация Паде является расширением полиномиальной аппроксимации, обеспечивающим повышенную точность представления функции. На рис. 11.2 представлен пример выполнения аппроксимации Паде с построением графика исходной функции (темная линия) и аппроксимирующей функции (более светлая линия).
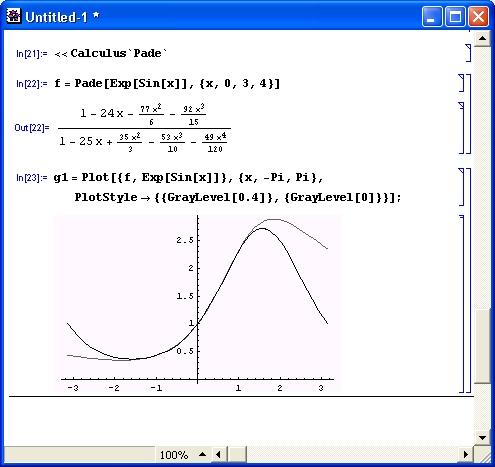
Рис. 11.2. Пример, осуществления аппроксимации Паде
