Вращение фигур на плоскости и в пространстве (Rotations)
Для задания поворота плоских фигур на заданный угол в подпакете Rotations заданы следующие функции:
- RotationMatrix2D[theta] – дает матрицу для поворота на угол theta в двух измерениях;
- Rotate2D [vec, theta] – поворачивает вектор vec по часовой стрелке на угол theta;
- Rotate2D[vec,theta,{x,y}] – поворачивает вектор vec по часовой стрелке на угол theta относительно точки с координатами {х, у}.
Рисунок 11.21 иллюстрирует работу с этими функциями.
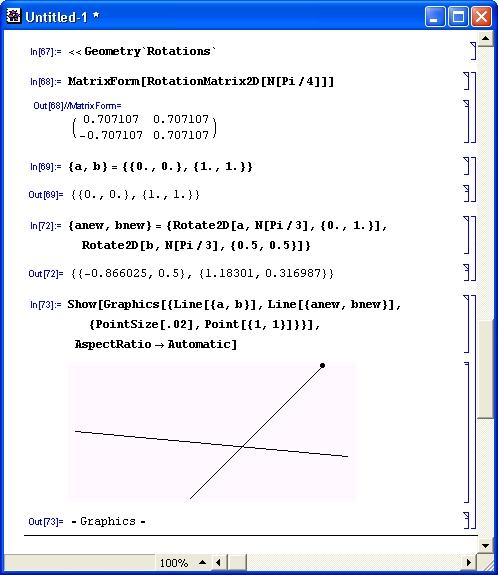
Рис. 11.21. Работа с функциями поворота
Аналогичные функции существуют и для поворота трехмерных фигур:
- RotationMatrix3D [psi, theta,phi] – дает матрицу поворота на заданные углы в трехмерном пространстве;
- Rotate3D [vec, psi, theta, phi] – поворачивает вектор vec на заданные углы в трехмерном пространстве;
- Rotate3D [vec, psi, theta, phi,{x,y,z}] – поворачивает вектор vec на заданные углы в трехмерном пространстве относительно точки с координатами {х,у, z}.
Приведем пример вычисления матрицы трехмерного поворота:
RotationMatrix3D[Pi, Pi/2, Pi/6] {{-(Корень из 3)/2.0.1/2 }},{1/2.0,(Корень из 3)/2},{ 0.1.0,}}