Пакет дискретной математики DiscreteMath. Комбинаторика и ее функции (Combinatorica и CombinatorialFunctions).
Следует отметить, что ввиду обилия функций даже в справочной системе даны примеры лишь для избранных функций. Для ознакомления с назначением конкретной функции достаточно исполнить команду ?Имя_функции, например:
<<DiscreteMath`Combinatorica` ?Permute Permute[l, p] permutes list 1 according to permutation p. ?KSubsets KSubsets[l, k] gives all subsets of set 1 containing exactly k elements, ordered lexicographically. KSubsets[{l, 2, 3, 4, 5}, 2] {{1, 2}, {1, 3), {1, 4}, {1, 5}, {2, 3), {2, 4}, {2, 5}, {3, 4}, {3, 5}, (4, 5}} << DiscreteMath`Combinatorica` MinimumChangePermutations[{1.2.3}] {{1, 2, 3}, {2, 1, 3}, {3, 1, 2}, {1, 3, 2}, {2, 3, 1}, {3, 2, 1}} Map[RankPermutation, Permutations[{1.2.3.4}]] {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23} InversePermutation[{4.8.5.2.1.3.7.6}] (5, 4, 6, 1, 3, 8, 7, 2} Polya[Table[ RotateRight[Range[8],i], {i,8}], m] 1/8 (4m+2m2 +m4 +m8) Table[NthSubset[n,a,b,c,d], {n,0.15}] {{}, {a}, {b}, {a, b}, {c}, {a, c}, {b, c}, {a, b, c}, {d}, (a, d}, {b, d}, {a, b, d}, {c, d}, {a, c, d}, {b, c, d}, {a, b, c, d}}Вторая группа функций комбинаторики представлена следующими функциями.
| Функции разделения, композиции и картин Янга | |
|---|---|
| CatalanNumber | Compositions |
| ConstructTableau | DeleteFromTableau |
| DurfeeSquare | EncroachingListSet |
| FerrersDiagram | FirstLexicographicTableau |
| . Insert IntoTableau | LastLexicographicTableau |
| Longest IncreasingSubsequence | NextComposition |
| Next Part it ion | NextTableau |
| NumberOf Compos it ions | NumberOf Partitions |
| NumberOf Tableaux | PartitionQ |
| Partitions | RandomComposition |
| RandomPartition | RandomTableau |
| TableauClasses | TableauQ |
| TableauxToPermutation | Tableaux |
| TransposePartition | TransposeTableau |
На рис. 11.6 показано несколько примеров работы с некоторыми из этих функций.
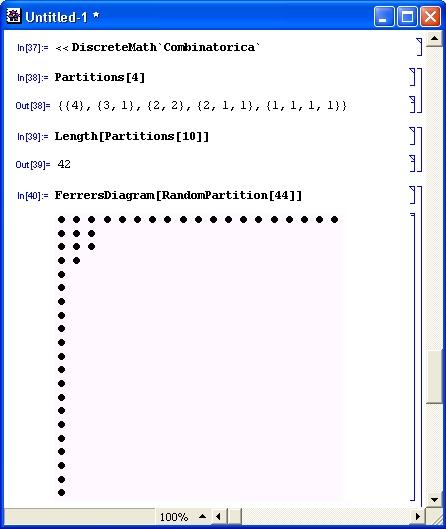
Рис. 11.6. Примеры работы с функциями разделения, композиции и картин Янга
Этих примеров достаточно, чтобы заинтересованный читатель по их образцу и подобию изучил свойства и возможности нужных ему функций комбинаторики.
